Soustava těles bez pasivních odporů řešená uvolňovací metodou

Zadání

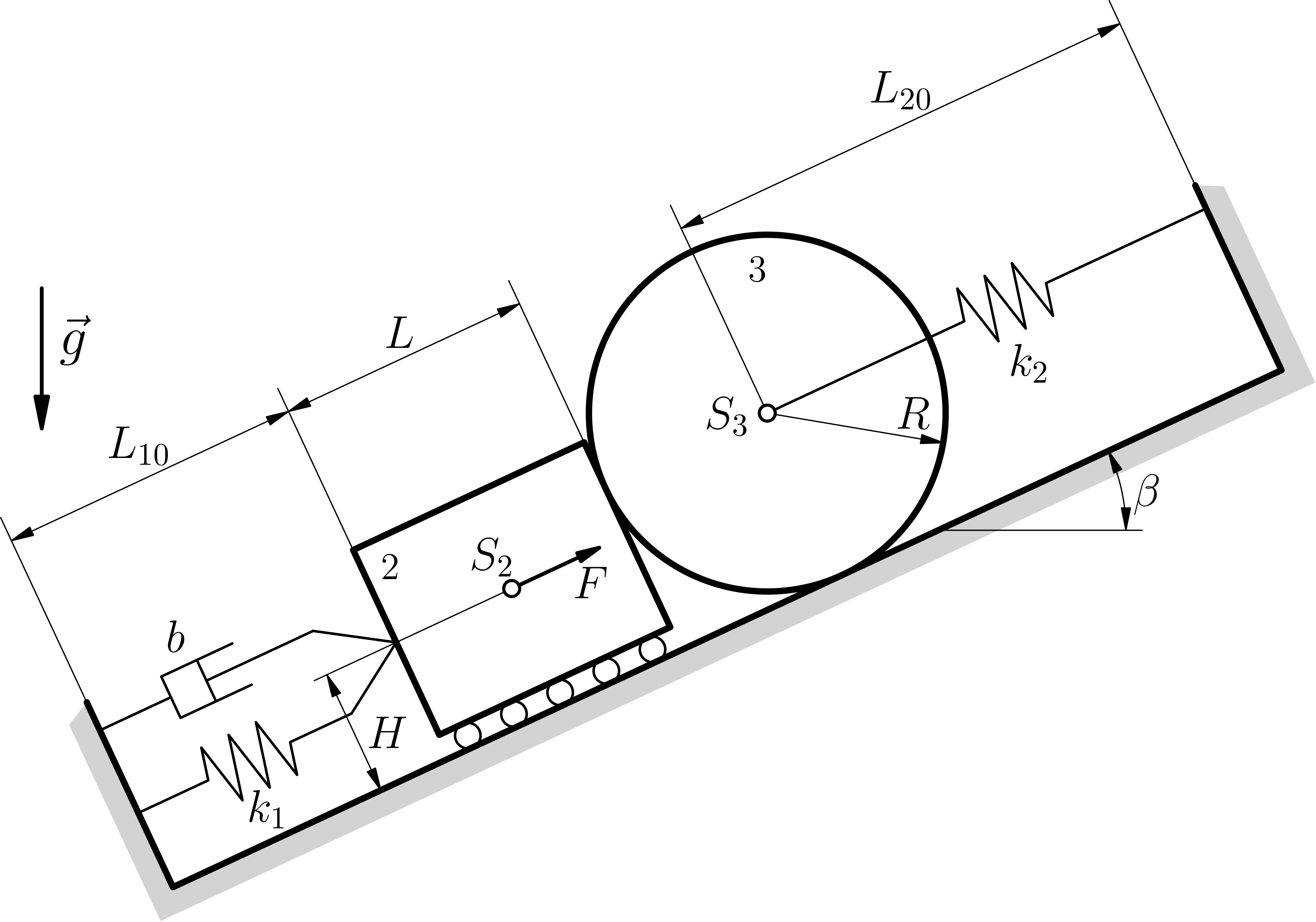
Soustava těles dle obrázku se pohybuje po nakloněné rovině bez uvažování pasivních odporů za pomoci zadané síly $F$. Sestavte pohybovou rovnici za použití uvolňovací metody.

Obrázek

nevyvazeny kotouc

$$ \newcommand{\dif}{\mathrm{d}} $$

Dáno: $\class{hmotnost}{m_2}$, $\class{hmotnost}{m_3}$, $\class{polomer}{R}$, $\class{vyska}{H}$, $\class{uhel_nakloneni}{\beta}$, $\class{moment_setrvacnosti}{J_{S3}}$, $\class{konstanta}{k_1}$, $\class{volna_delka}{L_{10}}$, $\class{konstanta}{k_2}$, $\class{volna_delka}{L_{20}}$, $\class{tlumeni}{b}$, $\class{soucinitel_treni}{(f)}$, $\class{sila}{F}$.

Odvoďte pohybovou rovnici.

Řešení

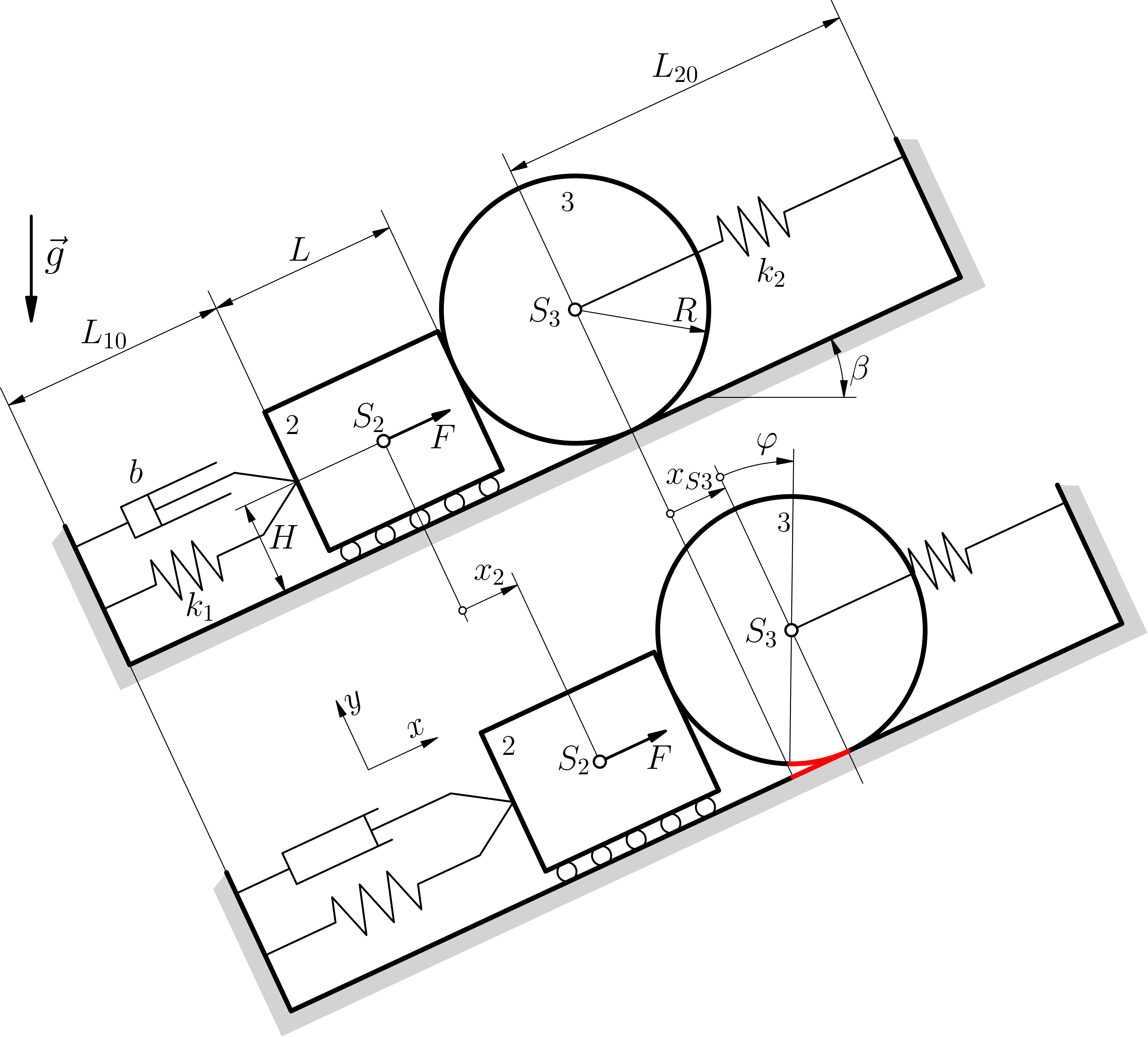
Protože zadání není zakresleno v obecné poloze, překreslíme si obrázek do obecné polohy a definujeme si polohy jednotlivých těles.
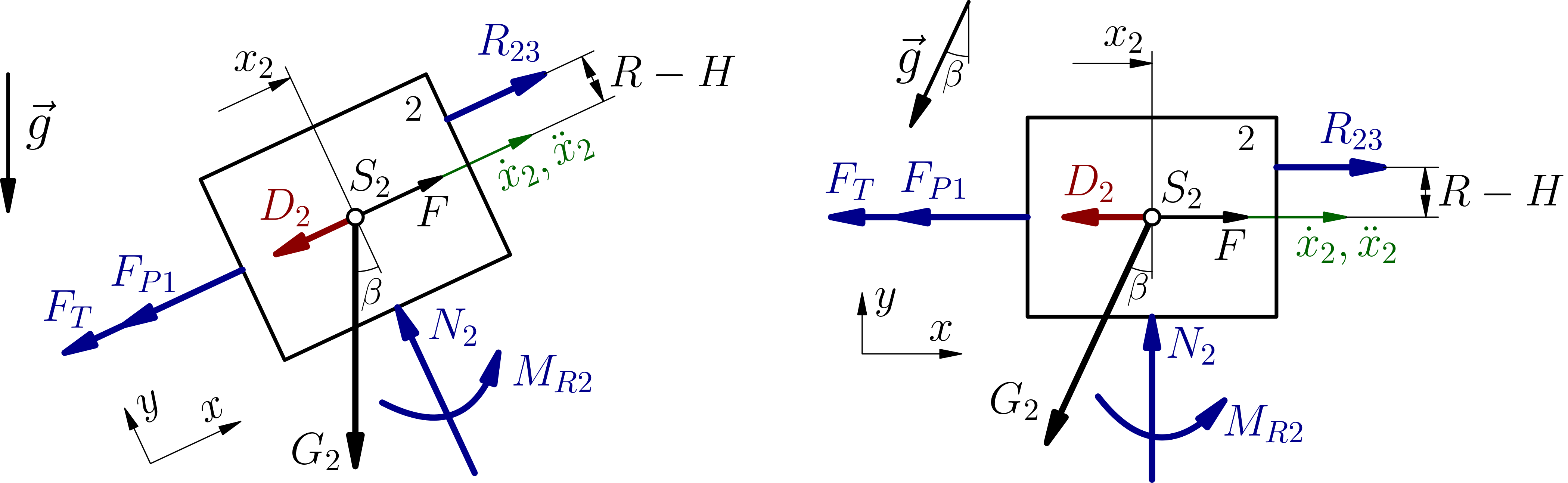
Tělesa uvolníme a v obecné poloze zakreslíme vnější a reakční síly známé ze statiky (reakce od podložky a sousedících těles, síly od pružin a tlumičů, tíhy, vnější zatížení, ...).
Určíme druh pohybu pro jednotlivá tělesa. V našem případě se těleso 2 pohybuje posuvným pohybem s kladnou rychlostí šikmo vpravo nahoru. Těleso 3 se pohybuje obecným rovinným pohybem s kladným smyslem úhlového zrychlení po směru hodinových ručiček.
Zakreslíme d'Alembertovu sílu $D_2$ do těžiště tělesa 2 $S_2$.
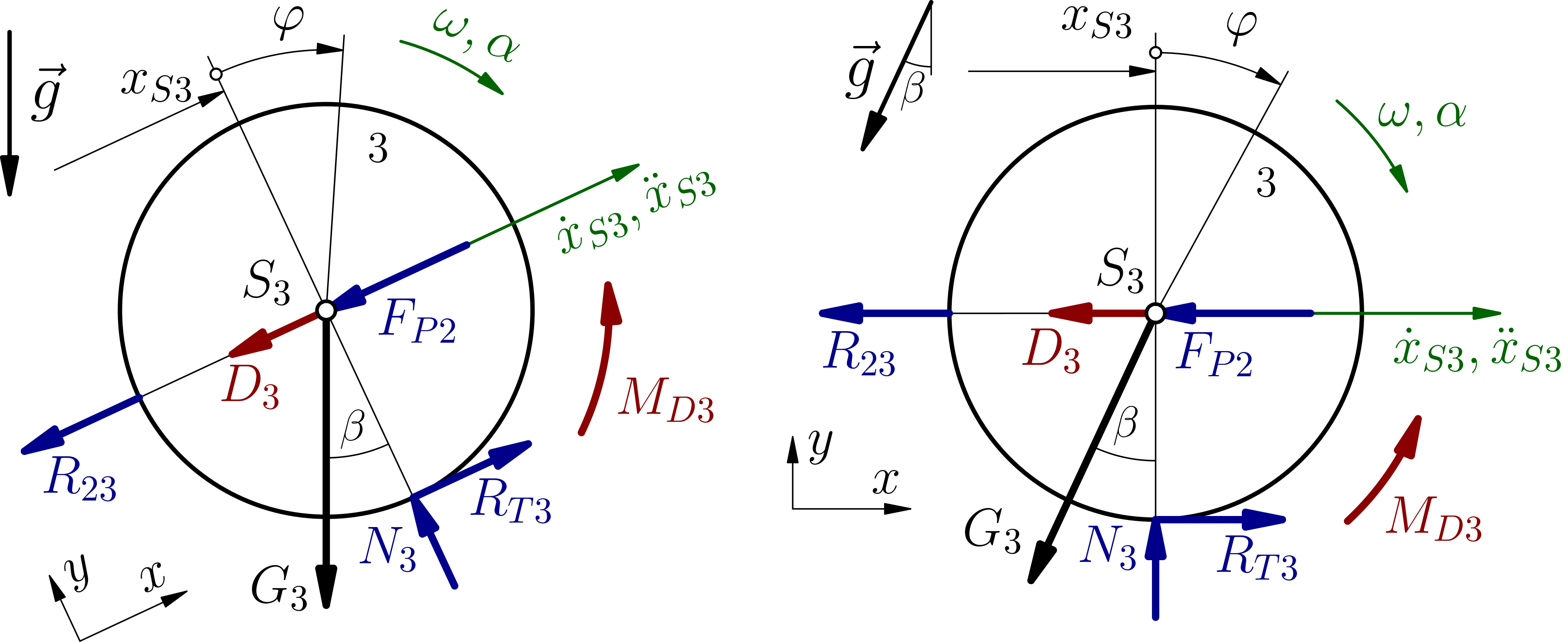
Zvolíme si referenční bod na tělese 3 (ideálně těžiště $S_3$). Zavedeme d'Alembertovu sílu $D_3$ do těžiště tělesa 3. Jelikož je referenční bod zároveň těžištěm tělesa 3, bude odstředivá a tečná dynamická síla rovna nule. Posledním dynamickým účinkem je tedy dynamický moment, působící proti úhlovému zrychlení.

Zakreslení v obecné poloze

nevyvazeny kotouc

Obrázek uvolnění

Těleso 2

nevyvazeny kotouc

Těleso 3

nevyvazeny kotouc

Rovnice dynamické rovnováhy sestavíme pro každé těleso zvlášť v lokálním souřadnicovém systému (x,y).

Pro těleso 2:

$$ \begin{align} \swarrow x &:\, F_{T}+F_{P1}+D_2-F-R_{23}+m_2\,g\sin(\beta)=0, \newline \nwarrow y &:\, N_2-m_2\,g\cos(\beta)=0, \newline \curvearrowright S_2 &:\, M_{R1}-R_{23}(R-H)=0. \end{align} $$

Pro těleso 3:

$$ \begin{align} \swarrow x &:\, R_{23}+D_3+F_{P2}-R_{T3}+m_3\,g\sin(\beta)=0, \newline \nwarrow y &:\, N_3-m_3\,g\cos(\beta)=0, \newline \curvearrowright S_3 &:\, M_{D3}+R_{T3}R=0. \end{align} $$

Specifikujme nyní jednotlivé síly, které jsme použili v rovnicích dynamické rovnováhy.

Síla v tlumiči je rovna součinu koeficientu tlumení $b$ a pístové rychlosti tlumiče $\dot{x}_2$

$$F_T=b\, \dot{x}_{2}.$$

Síla v pružině $F_{P1}$ je úměrná tuhosti $k_1$ a deformaci od volné délky. Vzhledem k vhodně zvolenému kótování polohy tělesa 2 je deformace pružiny právě rovna hodnotě $x_2$ a tedy

$$F_{P1}=k_1\,x_2.$$

d'Alembertova setrvačná síla $D_2$ je rovna součinu hmotnosti tělesa $m_2$ a zrychlení libovolného bodu na tělese (vycházíme z vlastností posuvného pohybu tělesa)

$$D_2=m_2 \, \ddot{x}_2.$$

d'Alembertova setrvačná síla $D_3$ je rovna součinu hmotnosti tělesa $m_3$ a zrychlení referenčního bodu $S_3$ na tělese 3 (vycházíme z vlastností obecného rovinného pohybu tělesa). Zrychlení

$$D_2=m_3 \, \ddot{x}_{S3}.$$

Síla v pružině $F_{P2}$ je úměrná tuhosti $k_2$ a deformaci od volné délky. Vzhledem k vhodně zvolenému kótování polohy tělesa 3 právě od volné délky je deformace pružiny rovna hodnotě $x_3$ a tedy

$$F_{P2}=k_2\,x_3.$$

Setrvačný (dynamický) moment $M_{D3}$ je roven součinu úhlového zrychlení a momentu setrvačnosti k referenčnímu bodu $S_3$

$$M_{D3}=J_{S3}\,\alpha.$$

Po dosazení do rovnic dynamické rovnováhy dostaneme:

$$ \begin{align} b\dot x_2 + k_1\,x_2 + m_2\,\ddot x_2-F-R_{23} + m_2\,g\sin{(\beta)} &=0 \qquad (1) \newline N_2-m_2\,g\cos(\beta) &=0 \qquad (2) \newline M_{R1}-R_{23}(R-H) &=0 \qquad (3) \newline R_{23}+m_3 \ddot x_{S3} + k_2 x_3 - R_{T3} + m_3 g \sin{( \beta )} &= 0 \qquad (4) \newline N_3-m_3\,g\cos(\beta) &=0 \qquad (5) \newline J_{S3}\,\alpha+R_{T3}R &=0 \qquad (6) \end{align} $$

Nyní máme soustavu 6 rovnic pro neznámé $ x_2$, $R_{23}$, $N_2$, $M_{R1}$, $\ddot x_{S3}$, $x_3$, $R_{T3}$, $N_3$, $\alpha $, tj. 9 neznámých.

Musíme pro řešení přidat kinematické rovnice: Vzdálenost $A$ mezi stěnami rámu je konstantní a v počáteční poloze ji lze zapsat jako $$L=L_{10}+L+R+L_{20},$$ zatímco v obecné poloze $$L=L_{10}+x_2+L+R-x_3+L_{20}.$$

Srovnáním obou výrazů dostaneme

\begin{equation} \cancel{L_{10}} + \cancel{L} + \cancel{R} + \cancel{L_{20}} = \cancel{L_{10}} + x_2 + \cancel{L} + \cancel{R} - x_3 + \cancel{L_{20}} \Rightarrow x_2 - x_3 = 0 \Rightarrow x_2 = x_3. \end{equation}

Polohu referenčního bodu $S_3$ lze vyjádřit jako $$x_{S3}=L_{10}+x_2+L+R,$$ což po dvojím zderivování dává

$$ \dot x_{S3}=\dot x_2 \rightarrow \ddot x_{S3}=\ddot x_2. $$

Třetí kinematickou rovnicí je vztah mezi zrychlením středu válce $\ddot x_{S3}$ a úhlovou rychlostí $\alpha$ při valení

$$ \ddot x_{S3}=R\,\alpha \Rightarrow \alpha=\frac{\ddot x_{S3}}{R}=\frac{\ddot x_{2}}{R} $$

Pohybovou rovnici sestavíme s pomocí rovnice (6), do které dosadíme za neznámou $R_{T3}$ z rovnice (4). Tím si ovšem přidáme neznámou $R_{23}$. Hodnotu $R_{23}$ lze přímo vyjádřit z rovnice (1).

$$(6) \rightarrow J_{S3} \frac{\ddot x_2}{R} + \,R_{T3} R = 0$$

$$(4) \rightarrow R_{T3}=R_{23}+m_3\,\ddot x_{S3}+k_2\,x_3+m_3\,g\sin(\beta) $$

$$(1) \rightarrow R_{23} = b\,\dot{x}_2 + k_1\,x_2 + m_2\,\ddot x_2-F+m_2\,g \sin{(\beta)} $$

Dosazením z kinematických rovnic dostaneme pohybovou rovnici: $$ J_{S3} \frac{\ddot{x}_2}{R} + \left( b \dot{x}_2 + k_1 x_2 + m_2 \ddot{x}_2 - F + m_2 g \sin{(\beta)} + m_3 \ddot{x}_2 + k_2 x_2 + m_3 g \sin{(\beta)} \right) R =0. $$

Rovnici vydělíme $R$ a seřadíme členy dle derivací $x_2$, čímž dostaneme hledaný konečný tvar pohybové rovnice:

$$ \ddot{x_2} \left( \frac{J_{S3}}{R^2} +m_2 + m_3 \right) \dot{x}_2 b +x_2\left( k_1 + k_2 \right) = F - g \sin{\beta} \left( m_2 + m_3\right). $$