Nevyvážený rotující kotouč

Zadání

Ventilátor se roztáčí na provozní otáčky \(\Omega\). Odpor lopatek ventilátoru je popsán pomocí odporového momentu \(M_O=k\omega^2\). Hnací moment \(M_H\) je konstantní. Vlivem poškození jedné z lopatek dojde k posunu těžiště od osy rotace o hodnotu \(e\). Určete velikost radiální reakce v uložení ventilátoru a sestavte pohybovou rovnici.

Obrázek

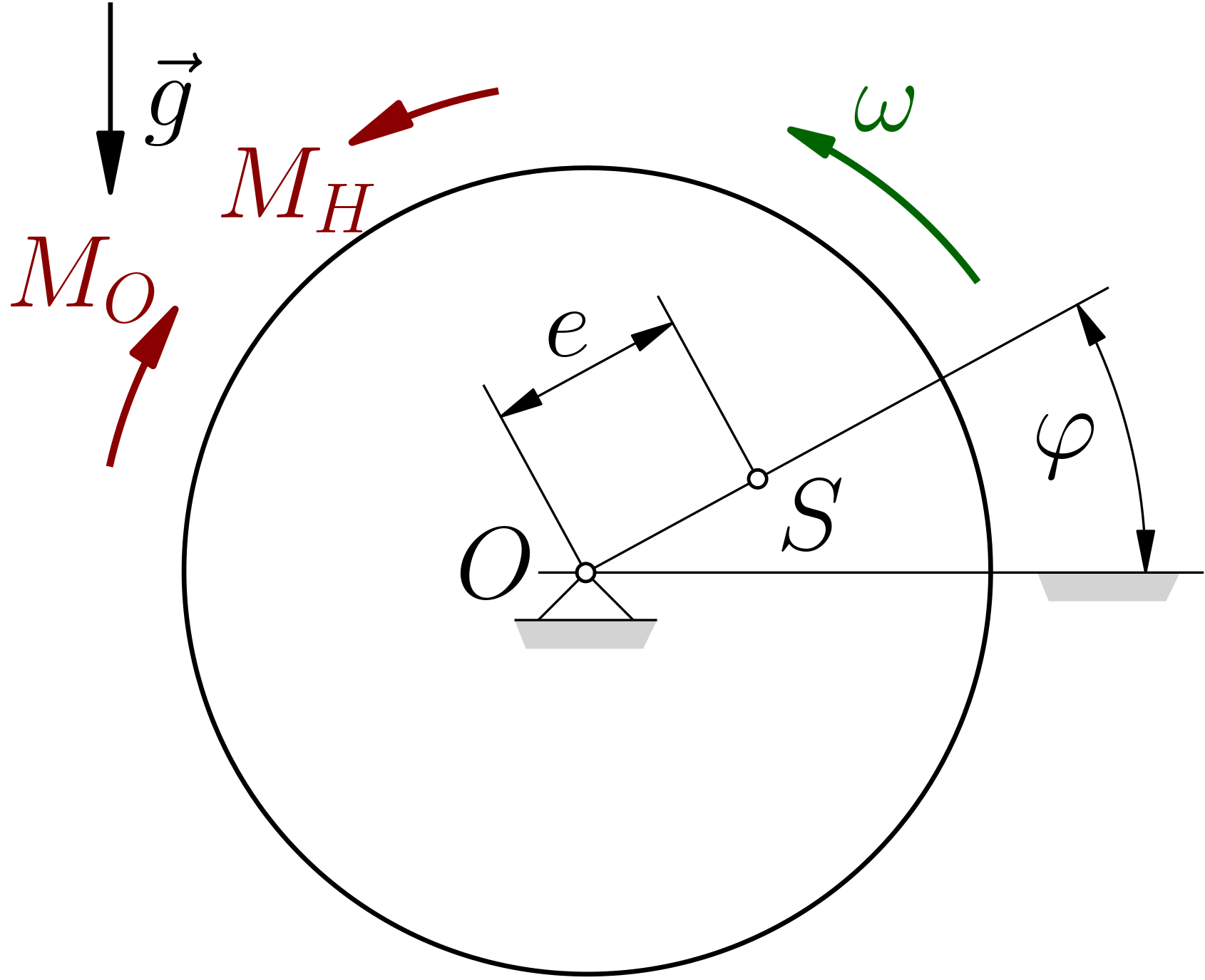
Dáno: \(\class{hmotnost}{m}\), \(\class{polomer}{R}\), \(\class{moment_setrvacnosti}{J_A}\), \(\class{konstanta}{k}\), \(\class{otacky}{\Omega}\), \(\class{excentricita}{e}\). Sestavte rovnice rovnováhy.

Řešení

Za referenční bod zvolíme takový bod, který se z pohledu kinematiky pohybuje co nejjednodušším způsobem. Osa rotace \(O\) kotouče je bodem tělesa, který se nepohybuje a proto jej zvolíme za referenční bod. Rychlost a zrychlení referenčního bodu je tedy v našem případě nulové (\(a_O=0\) a \(v_O=0\)).

Obrázek uvolnění

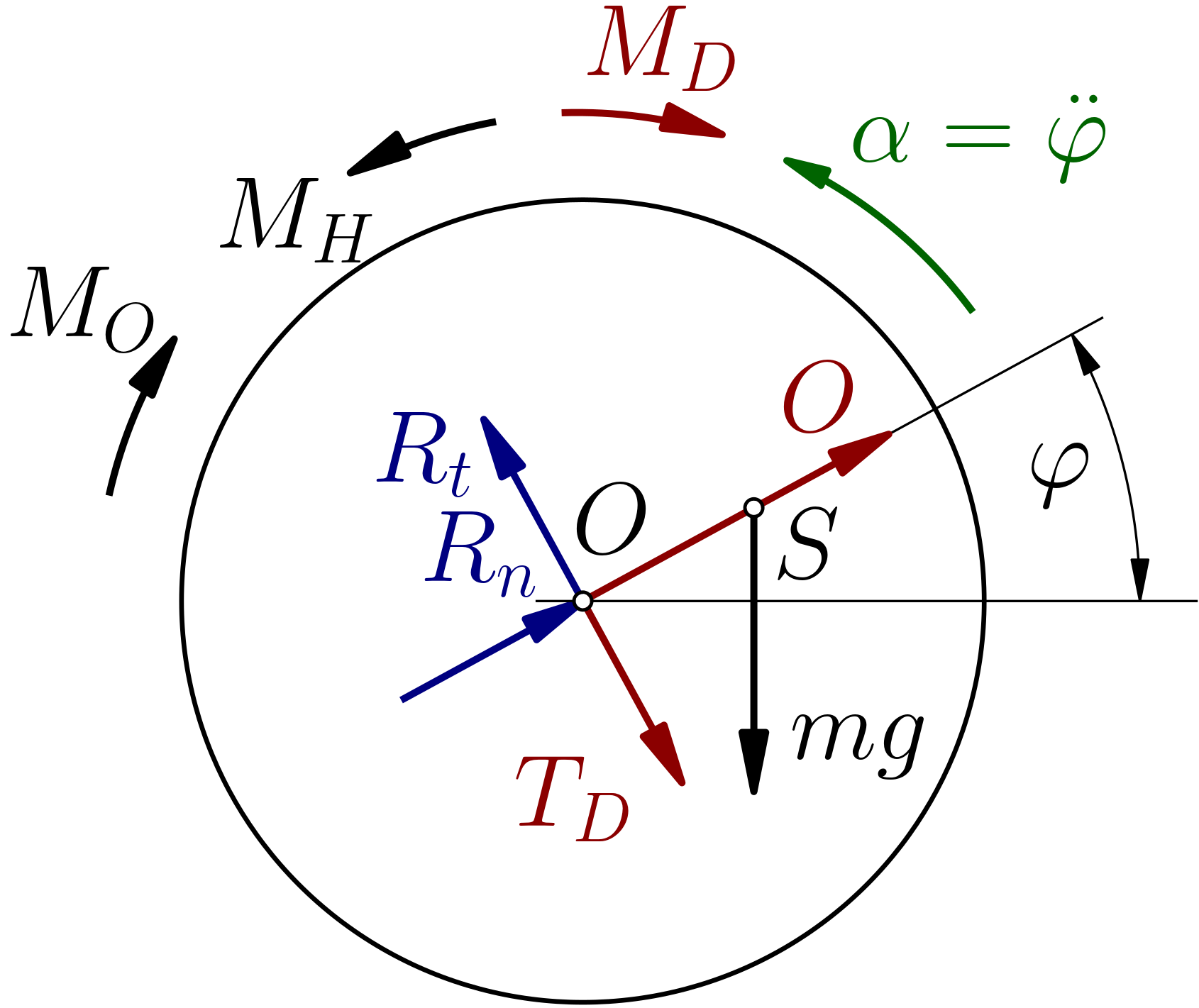
Zrychlení referenčního bodu je rovno nule, proto bude d'Alembertova síla $$D=m\, a_O=0.$$

Rovnice dynamické rovnováhy sestavíme v lokálním souřadnicovém systému (t,n): $$ \begin{align} \nearrow n &:\, R_n+O-m\,g\, \sin(\varphi)=0, \newline \nwarrow t &:\, R_t-T_D-m\,g\, \cos(\varphi)=0, \newline \curvearrowright O &:\, -M_H+M_O+M_D+m\, g\, e\, \cos(\varphi)=0. \end{align} $$

Úhlové zrychlení spočítáme jako druhou derivaci natočení $$\alpha=\frac{\mathrm{d} \omega}{\mathrm{d} t}=\ddot{\varphi}$$ a potom bude tečná dynamická síla rovna $$T_D=m \,e \, \alpha=m \,e \, \ddot{\varphi}.$$ Odstředivá síla bude $$O=m\, e\, \omega^2=m\, e\, \dot{\varphi}^2$$ Setrvačný moment určíme jako součin momentu setrvačnosti a úhlového zrychlení, tedy $$M_D=J_A \,\alpha=J_A \,\ddot{\varphi}.$$

Po dosazení do rovnic dynamické rovnováhy dostaneme

$$ \begin{align} \nearrow n &:\, R_n+m\, e\, \dot{\varphi}^2-m\,g\, \sin(\varphi)=0, \newline \nwarrow t &:\, R_t-m \,e \, \ddot{\varphi}-m\,g\, \cos(\varphi)=0, \newline \curvearrowright O &:\, -M_H+k\dot{\varphi}^2+J_A \,\ddot{\varphi}+m\, g\, e\, \cos(\varphi)=0. \end{align} $$

Řešením soustavy rovnic získáme vztahy pro reakce

$$ \begin{align} R_n &=-m\, e\, \dot{\varphi}^2+m\,g\, \sin(\varphi), \newline R_t &= m \,e \, \ddot{\varphi}+m\,g\, \cos(\varphi). \end{align} $$

Pohybovou rovnici sestavíme z rovnice dynamické momentové rovnováhy $$ \ddot{\varphi}\,J_A+\dot{\varphi}^2\, k+\cos(\varphi)\, m\, g\, e=M_H$$